【Python実装】HMM(隠れマルコフモデル)を構造化変分ベイズで推論
今回は、HMM(隠れマルコフモデル)の構造化変分ベイズ推論をPythonで実装します。
モデルと推論方法に関しては、書籍「ベイズ推論による機械学習(須山)」の5-3章を参考にしています。詳しい途中計算はこちらをご参照ください。

機械学習スタートアップシリーズ ベイズ推論による機械学習入門 (KS情報科学専門書)
- 作者: 須山敦志,杉山将
- 出版社/メーカー: 講談社
- 発売日: 2017/10/21
- メディア: 単行本(ソフトカバー)
今回のコードをgithubに載せています。 githubはこちら
Twitterフォローよろしくお願いいたします! twitterはこちら
HMM(隠れマルコフモデル)とは?
HMMとは、観測データの背後にある潜在変数\({\bf S}=\{s_1,s_2,...,s_N\}\)の離散的な系列変化を仮定したモデルです。時系列データに対するモデリングとして広く利用されています。
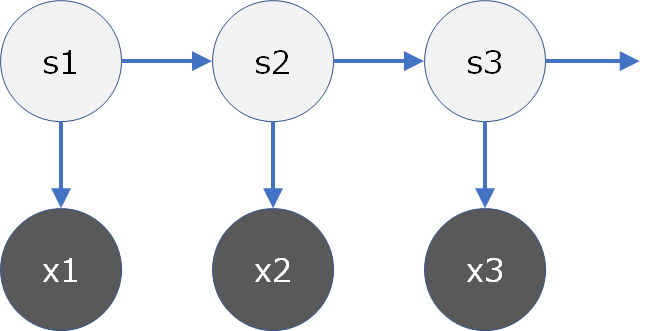
観測モデル\({\bf X}\)と潜在変数の状態系列モデル\({\bf S}\)から成り立ちます。
今回は簡単のため、\(s_n\)が1時点前の\(s_{n-1}\)のみに依存する1次マルコフモデルを仮定します。
状態系列モデル
$$p(s_n|s_{n-1}, {\bf A})=\prod_{i = 1}^{K} Cat({\bf s}_n|{\bf A}_{:,i})^{s_{n-1}, i}$$$$p(s_1|\boldsymbol\pi)=Cat(s_1|\boldsymbol\pi)$$初期確率\(\boldsymbol\pi\)と遷移確率行列の列\({\bf A}_{:,i}\)にも各々ディリクレ分布で事前確率を与えます。
実務では\({\bf A}_{:,i}\)について、ドメイン知識を入れ込める場合が多いです。十分な学習に必要なデータ数の削減や精度の安定化ができることがあり、ベイズ学習の強みの一つといえます。
観測モデル
今回は書籍に則り、ポアソン観測モデルによる隠れマルコフモデルを仮定します。$$p(x_n|s_n)=\prod_{k = 1}^{K} Poi(x_n|\lambda_k)^{s_n, k}$$\(\lambda_k\)にも共役事前分布のガンマ分布で事前確率を与えます。観測モデルは、タスクに応じて自由に設定します。
観測変数\({\bf x}\)のみを使用して、未知の潜在変数\({\bf S}\)と各パラメーター\(\boldsymbol\lambda, {\bf A}, \boldsymbol\pi\)の事後分布を構造化変分ベイズ推論します。
構造化変分ベイズとは?
まず変分ベイズとは、複雑な事後分布を簡単な分布で近似するために2分布間のKLダイバージェンスを最小化する、またはELBO(変分下限)を最大化する推論方法です。最適化問題に帰着するため、MCMCと比べて計算が高速です。
変分ベイズでは計算を簡易化するため、推論したい潜在変数・パラメーターを全て独立と仮定する「平均場近似」による「完全分解変分ベイズ」が一般的に利用されています。
しかしそれでは、隣り合う潜在変数同士が相関を持つというHMMの仮定に反することになるため、今回は潜在変数同士は独立に分解せずに同時分布として扱う「構造化変分ベイズ」にて推論を実施します。
- 完全分解変分ベイズ$$p({\bf S}, \boldsymbol\lambda, {\bf A}, \boldsymbol\pi) \approx \{\prod_{n = 1}^{N} q(s_n)\} q(\boldsymbol\lambda, {\bf A}, \boldsymbol\pi)$$
- 構造化変分ベイズ(今回実施。\(q({\bf S})\)が同時分布)$$p({\bf S}, \boldsymbol\lambda, {\bf A}, \boldsymbol\pi) \approx q({\bf S})q(\boldsymbol\lambda, {\bf A}, \boldsymbol\pi)$$
フォーワード・バックワードアルゴリズム
\(q({\bf S})\)の同時分布を求めるといっても、\(q(\boldsymbol\lambda, {\bf A}, \boldsymbol\pi)\)の計算に\(s_n\)と \(s_{n-1} \rightarrow s_n\)の期待値が必要で、\(q(s_n), q(s_n, s_{n-1}),\)を使って算出するのですが、構造化変分ベイズの計算過程の中で\(q(s_n), q(s_{n-1},s_n)\)を個別に計算できるわけではないため、\(q({\bf S})\)を求めた後に周辺化して求める必要があります。
しかし単純に周辺化すると、\({\bf S}=\{s_1,s_2,...,s_N\}\)は観測データ数と同数あるため、計算量が爆発してしまいます。
この時、フォワード・バックワードアルゴリズムという手法が便利です。HMMのグラフィカルモデルの特徴の恩恵(\(x_t\perp s_{t+1}|s_t\), \(s_{t+1}\perp s_{t-1}|s_t\))を受け、計算量を削減することができます。ベイズ推論でお馴染みの「事後分布→結合分布→着目変数項以外を定数化」の流れで以下導出。\(f(s_n)\)と\(b(s_n)\)に分解できます。
$$q(s_n)=\sum_{{\bf S_{\backslash n}}}q({\bf S}) \propto \sum_{{\bf S_{\backslash n}}}\tilde{p}({\bf X_{1:n}}, {\bf S_{1:n}})=f(s_n)b(s_n)$$$$f(s_n)=\tilde{p}(x_n|s_n)\sum_{{\bf S_{1:n-1}}}\tilde{p}(s_n|s_{n-1})\tilde{p}({\bf X_{1:n-1}},{\bf S_{1:n-1}})$$$$b(s_n)=\sum_{{\bf S_{n+1:N}}}\tilde{p}({\bf X_{n+1:N}},{\bf S_{n+1:N}}|s_n)$$
さらに詳しく分解すると、以下のように再帰式が得られます。計算量が\(O(N)\)に削減できています。
- フィードフォワード(前向き)$$f(s_n)=\tilde{p}(x_n|s_n)\sum_{{\bf S_{n-1}}}\tilde{p}(s_n|s_{n-1})f(s_{n-1})$$
- バックワード(後向き)$$b(s_n)=\sum_{{\bf S_{n+1}}}\tilde{p}(x_{n+1}|s_{n+1})\tilde{p}(s_{n+1}|s_n)b(s_{n+1})$$
実装
Pythonにて実装しました。主にnumpyで書いています。データは自分で作成しました。
今回のコードをgithubに載せています。 githubはこちら
HMMの構造化変分推論のみ貼ります。
import numpy as np import math from scipy import special as sp from scipy import stats as st def HMM_paredict_s(x, K=3, iter_num=20, my_seed=0): #set seed np.random.seed(seed=my_seed) # sample num N=len(x) ### prior parameters # gamma distribution a=200 b=5 # Dirichlet distribution for \pi alpha = np.array([30,20,10]) # Dirichlet distribution for \A beta = np.array([[20,10,10],[10,20,10],[10,10,20]])
### posterior parameters # gammma distribution a_update = np.array([200,200,200]) b_update = np.array([5,5,5]) # Dirichlet distribution for \pi alpha_update = np.array([30,20,10])
# Dirichlet distribution for \A beta_update = np.array([[20,10,10],[10,20,10],[10,10,20]]) # set state value first value s_mean=[] for n in range(N): s_mean.append([0.4,0.3,0.3]) s_mean = np.array(s_mean) for i in range(iter_num): ##################################################### # expectation of λ、π、A lam_mean=np.zeros(K) ln_lam_mean=np.zeros(K) ln_pi_mean=np.zeros(K) ln_A_mean=(np.zeros((K,K))).tolist() lam_mean = a_update/b_update ln_lam_mean=sp.digamma(a_update)-np.log(b_update) ln_pi_mean=sp.digamma(alpha_update)-sp.digamma(np.sum(alpha_update)) ln_A_mean = sp.digamma(beta_update) - sp.digamma(np.sum(beta_update, axis=0)) ##################################################### # q(Sn)、q(Sn, Sn-1) p_xn_sn_array =np.zeros((N, 3)) # forward algorithm f_pass = np.zeros((N, 3)) for n in range(N): ln_xn_sn = x[n]*ln_lam_mean-lam_mean p_xn_sn = np.exp(ln_xn_sn) p_xn_sn/=np.sum(p_xn_sn) p_xn_sn_array[n] = p_xn_sn p_s1 = np.exp(ln_pi_mean) p_s1/=np.sum(p_s1) p_sn_sn_1 = np.exp(ln_A_mean) p_sn_sn_1 /=np.sum(p_sn_sn_1, axis=0) if n==0: f_pass[n] = p_xn_sn * p_s1 else: f_pass[n] = p_xn_sn * np.sum(f_pass[n-1] * p_sn_sn_1, axis=1) f_pass[n] /=sum(f_pass[n]) # backward algorithm b_pass = np.zeros((N, 3)) for n in reversed(range(N)): if n==N-1: b_pass[n] = np.ones(3) else: ln_xn_sn = x[n+1]*ln_lam_mean-lam_mean p_xn_sn = np.exp(ln_xn_sn) p_xn_sn/=np.sum(p_xn_sn) p_sn_sn_1 = np.exp(ln_A_mean) p_sn_sn_1 /=np.sum(p_sn_sn_1, axis=0) b_pass[n] = np.sum(b_pass[n+1].reshape(3,1) * p_sn_sn_1 * p_xn_sn.reshape(3,1), axis=0) b_pass[n] /=sum(b_pass[n]) s_mean = f_pass * b_pass s_mean /=np.sum(s_mean, axis=1).reshape(N, 1) f_sn_1_b_sn = f_pass[1:].reshape(len(f_pass[1:]), 1, 3) * b_pass[:-1].reshape(len(b_pass[:-1]), 3, 1) s_s_1_mean = f_sn_1_b_sn * p_sn_sn_1 * p_xn_sn_array[1:].reshape(len(p_xn_sn_array[1:]), 3,1) s_s_1_mean = s_s_1_mean/np.sum(s_s_1_mean, axis=1).reshape(N-1,3,1) ########################################### # update a, b a_update = np.sum(x.reshape(len(x),1) * s_mean, axis=0) + a b_update = np.sum(s_mean, axis=0) + b # update α alpha_update = s_mean[0] + alpha # update β beta_update = np.sum(s_s_1_mean + beta, axis=0) ##################################################### # determine group number(just, symbol) by order of λ s_order = st.gamma(a=a_update, scale=1/b_update).mean().argsort() s_mean_ordered = s_mean[:,s_order] return s_mean_ordered
実験&結果
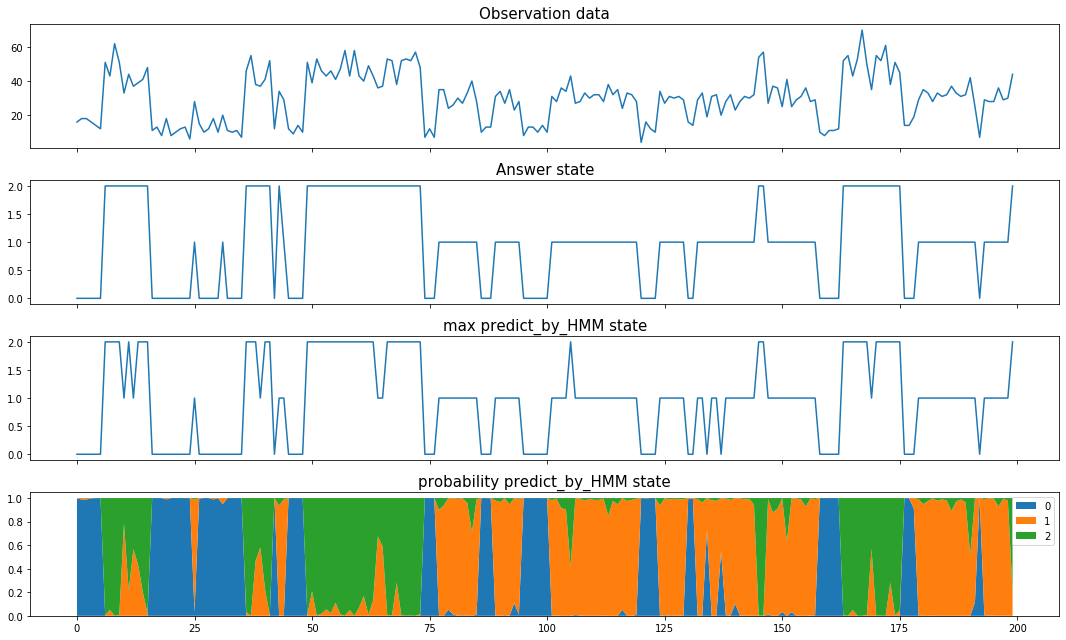
観測変数とモデルのみで潜在変数を予測しました。モデルで仮定した生成過程と実際のデータの生成過程が同じであるため当たり前ですが、潜在変数の正答率は94.5%でした。1列目が観測データ、2列目が正解の潜在変数、3列目が予測確率が最大になるカテゴリー、4列目が各カテゴリーの予測確率を表しています。
パターン別のHMMとPMM(ポアソン混合モデル)比較実験
次に、潜在変数のマルコフ性を仮定しないポアソン混合モデル(PMM)との比較実験を紹介します。以下、パラメーターにも事前分布をもたしています。

観測モデルである3つのポアソン分布の\(\lambda\)の値が近づいて差異を少なくしていった時のHMMとPMMの精度を比較しました。ポアソン混合モデルは完全分解変分ベイズで推論しています。

下が結果です。

図の通り、ポアソン分布の\(\lambda\)の値が近づいてくると、時系列情報のおかげでHMMの方が、精度が高く推論できています。
今回のコードをgithubに載せています。 githubはこちら
Twitterフォローよろしくお願いいたします! twitterはこちら